Admin
Admin


 عدد المساهمات : 34923 عدد المساهمات : 34923
نقاط : 160759
السٌّمعَة : 1074
تاريخ التسجيل : 14/05/2009
الموقع : http://www.autoformer.net/
 |  موضوع: Ensemble et application (partie III موضوع: Ensemble et application (partie III  الثلاثاء سبتمبر 28 2010, 13:25 الثلاثاء سبتمبر 28 2010, 13:25 | |
| attendez quelques secondes jusqu'au chargement de la page complete  I. Famille 1. Définition I. Famille 1. Définition Soit 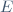 et 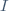 deux ensembles non vides, on appelle famille d'éléments de 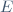 indexés par 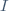 toute application :  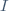 sera appelé l'ensemble des indices.  sera noté :  et l'application 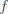 sera noté :  . Remarque : Si  , la famille  s'appelle suite d'éléments de 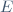 . 2. Opérations sur les familles Soient 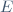 un ensemble et 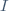 ensemble des indices  ; soit  la famille des parties de 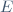 , on définit :
- Intersection :
 . .
- Réunion :
 . .
3. Partition d'un ensemble Soient 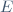 et 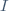 deux ensembles non vides, soit  une famille d'éléments de  . On dit que  est une partition de 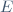 si :
-
 . .
-
 . .
-

Exemple : Soit :  et  ,  ,   est une partition de 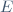 . II. Relation Binaire 1. Définition Soit 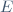 un ensemble non vide et  un graphe. On appelle relation binaire definie sur 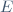 toute correspondance de 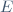 et on note :  . On note aussi  et on dit que :  est en relation avec  . 2. Propriétés éventuelles d'une relation binaire Soit  une relation binaire sur un ensemble 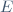 non vide.  est dite :
- Réflexive si :
 , ,  . .
- Symétrique si :
 : :  . .
- Transitive si :
 : :  et et  . .
- Antisymétrique si :
 : :  et et  . .
3. Relation d'équivalence - Relation d'ordre Soit 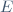 un ensemble non vide et soit  une relation binaire définie sur 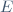 . On dit que :
 est une relation d'équivalence si elle est : Réflexive - Symétrique - Transitive. est une relation d'équivalence si elle est : Réflexive - Symétrique - Transitive.
 est une relation d'ordre si elle est : Réflexive - Antisymétrique - Transitive, et dans ce cas, est une relation d'ordre si elle est : Réflexive - Antisymétrique - Transitive, et dans ce cas,  sera noté sera noté  s'il n'y a pas de risque de confusion avec une situation usuelle. s'il n'y a pas de risque de confusion avec une situation usuelle.
4. Classe d'équivalence - Ensemble quotientSoit 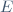 un ensemble non vide muni d'une relation d'équivalence  et soit  .
- L'ensemble
 est appelé classe d'équivalence de est appelé classe d'équivalence de  et on note généralement : et on note généralement :  ou ou  . .
- L'ensemble des classes d'équivalence s'appelle ensemble quotient noté :
 . .
Proposition : Soit  un ensemble non vide et soit  une relation d'équivalence définie sur  , alors :  forme une partition de  . 5. Ensemble Ordonné Soit 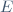 un ensemble non vide muni d'une relation d'ordre  , on dit alors que  est un ensemble ordonné. Et dans ce cas, pour  , on dit que :
-
 et et  sont comparables si : sont comparables si :  ou ou  . .
-
 est un ensemble totalement ordonné si tous les éléments de est un ensemble totalement ordonné si tous les éléments de 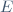 sont comparables, sinon, sont comparables, sinon,  est partiellement ordonné. est partiellement ordonné.
6. Eléments particuliers Soit  un ensemble ordonné et soit  , on dit que :
-
 est le plus grand élément de est le plus grand élément de 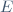 (si il existe) si : (si il existe) si :  et on note et on note  . .
-
 est le plus petit élément de est le plus petit élément de 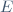 (si il existe) si : (si il existe) si :  et on note et on note  . .
7. Majorant et Minorant d'une partie Soit  un ensemble ordonné avec 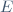 non vide et soit  avec  , on dit que :
-
 est majorée si : est majorée si :  . .
-
 est minorée si : est minorée si :  . .
| |
|








